Data Structures
A Basic Overview of the Basic Data Structures used in Computer Science
Introduction to Data Structures
In this era of tech evolution where every click is recorded, ever wondered how this data collected is organized and stored in systems so that it can be efficiently accessed and updated? This is where data structures come into play. Here, efficiency means in terms of access time and space.
Data at its basic level is just 0s and 1s. It is up to us how we interconnect and represent information with them. If data is arranged systematically then it gets a structure and becomes meaningful. This meaningful or processed data is called information. Data structures help us in organizing the data in a way it can be used efficiently. They are a way how to play with memory and use it efficiently in terms of both space and access time.
Data structures are very important to organize the data. An algorithm is problem-solving. The problem takes some input and creates some output. The input and output should be given in some format. This format is called a data structure. Depending on the format the memory space occupied and the access time of the algorithm varies.
Types of Data Structures

Classifying data structures gives us different ways of accessing and storing data in different ways. Each data structure type is suitable for a particular kind of problem.
Depending on the in-memory representation, data structures divide into two categories:
Linear data structure
Non-linear data structure
Linear data structures
Linear data structures are arranged on a single level sequentially (linearly). The data structure is easy to implement and traverse because it imitates computer memory arrangement. Linear data structures branch further into two subcategories based on memory allocation changes:
Static data structures have a fixed size. Elements can change order, but the memory allocation for the data structure stays the same. Example: Array
Dynamic data structures have a modular size. Runtime changes allow altering the data structure size. The nodes here are created using structures and linked using pointers. Structures can be created dynamically. Example: linked list, stack, queue
Array
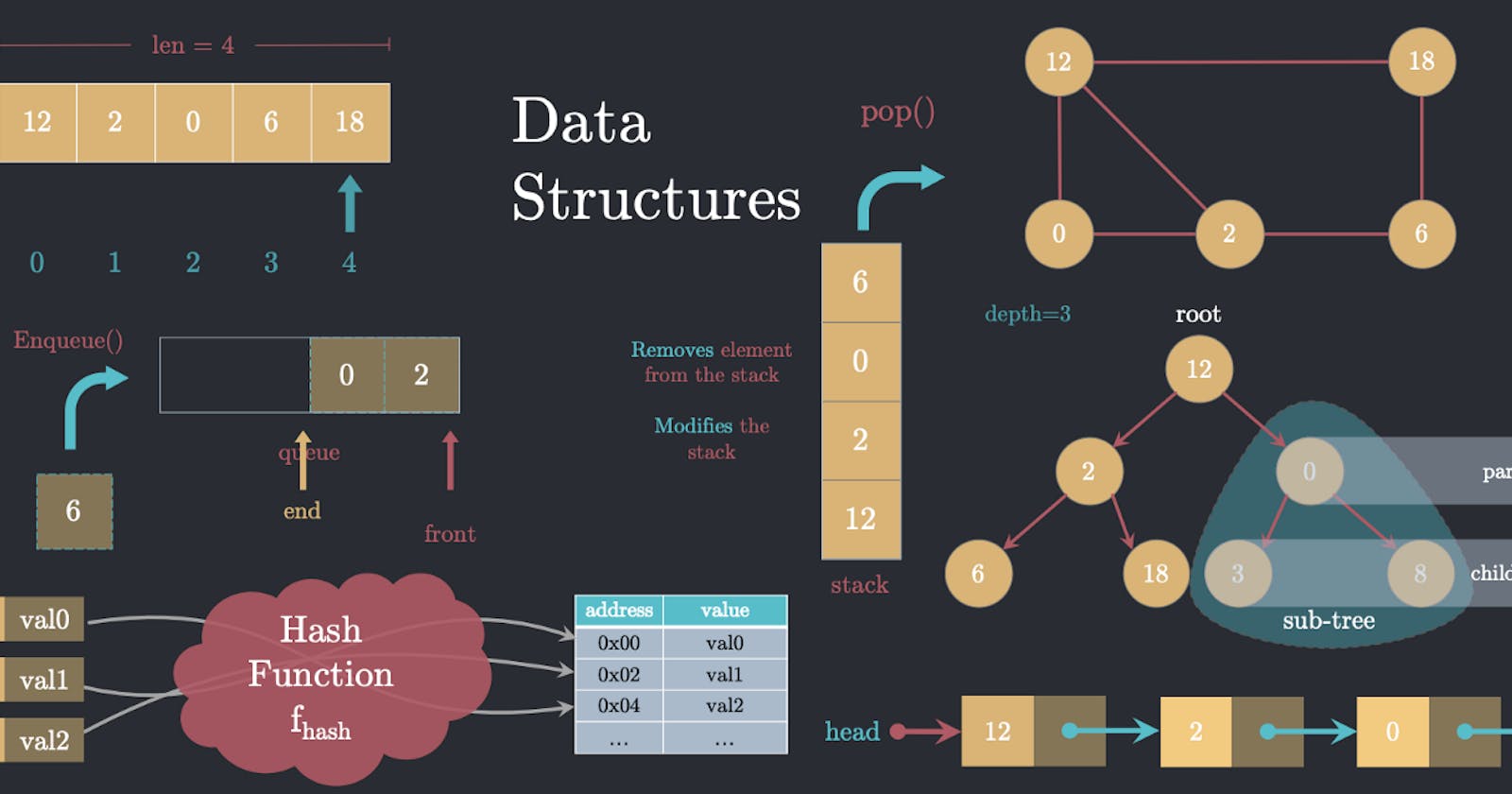
Arrays are the basic and simplest data structures in most programming languages which are randomly accessed. It means we can go to any element directly without crossing all the elements. It happens because an array is stored in the memory in a contiguous manner. An array consists of a sequence of elements of the same type.
The sequential numbering of data in an array's elements from first to last is called an index. Generally, the index starts from 0 as it is more logical. Elements are items stored in an array and can be randomly accessed by their index. The length of an array is determined by the number of elements it can contain. The length of an array is known in advance and cannot change.
How the elements will be represented in an array is decided at the time of declaration. Memory allocation of an array of a given size is also done at the time of declaration.
How is random access possible?
In an array, we know the starting address which is called the base address and the size of each element in the array. The size of each element depends on the data type of the elements stored in the array. Let's consider an array "arr" and we want o access the element in the index "i".
Number of bytes we have to cross from the base address to reach the element = i * size of each element
address of arr[i] = base address + i * size of each element
One dimensional array

Multi-dimensional array

The way we conceptually think of a multi-dimensional array and the way they are stored in memory is completely different. If we store it as it is in the memory then after each row there will be a lot of blank space. Thus random access will fail as we will have no clue how to access the next row after each row. To have random access we have to store the array in the memory in a contiguous manner. Thus we have to convert the multi-dimensional array to a one-dimensional array.
Multi-dimensional arrays can be stored in memory in 2 ways
Row major order
Column major order

Linked List
Here the elements are not stored in contiguous memory locations. Hence random access fails. It is made up of nodes. These nodes are generally self-referential structures. It means every structure will have a pointer inside it. This pointer will point to a structure of the same type. The head pointer always points to the first element in the list.
In the linked list we have sequential access. It means to access an element we have to start from the beginning and travel through the entire list.
Arrays cannot be created dynamically. Using structures the advantage is that the data structures can be created dynamically. Hence, if we lose the address we also lose access to the node.
Single-linked list: Every node has a single link pointing to the next node.

Circular linked list: Here, the first node and the last node are connected which forms a circle. There is no NULL at the end.

Doubly linked list: Along with the NEXT pointer it also has a PREV pointer

Circular Doubly linked list: It has properties of both a doubly linked list and circular linked list in which two consecutive elements are linked or connected by the PREV and NEXT pointer and the last node points to the first node by the NEXT pointer and also the first node points to the last node by the PREV pointer.

Array vs Linked List
| Array | Linked List |
| Arrays are stored in a contiguous location | Linked lists are not stored in a contiguous location |
| Fixed in size | Dynamic in size |
| Memory allocated at compile time | Memory allocated at run time |
| Uses less memory than linked lists | Uses more memory because it stores both data and pointers to the next node |
| Random access is possible | Random access is not possible. To access an element we have to traverse the whole linked list |
| Array elements are independent of each other. | Linked list elements are dependent on each other. As each node contains the address of the next node so to access the next node, we need to access its previous node. |
Stack
A stack is a sequence of piled elements and we can think of it like a stack of trays. It is a linear data structure. Adding or removing elements occurs from the top of the stack, making it a Last In First Out (LIFO) structure. The last added element is also the first one removed

Basic operations that can be performed using a stack
push() to insert an element into the stack
pop() to remove an element from the stack
top() Returns the top element of the stack.
isEmpty() returns true if the stack is empty else false.
size() returns the size of the stack.
Implementation: The stack can be implemented either using an array or a linked list.
Applications of stack
Recursion
Infix-postfix conversion
Parsing: Matching parenthesis/matching tags
Browsers: All the pages or links we have visited are arranged in a stack
Editors (undo and redo operations)
Tree traversals and graph traversals
Queue

We can compare queues to waiting lines. Just like a stack, a queue is also a linear data structure. In a stack, we insert and delete elements from the same side. A queue is open at both ends. Here, we insert elements from one side and delete elements from the other side. Queues are a First In, First Out (FIFO) data structure when it comes to adding and removing elements.
Front: the index where the first element is stored in the array representing the queue.
Rear: the index where the last element is stored in an array representing the queue.
Basic operations that can be performed using a stack
enqueue() Adding elements
dequeue() Removing elements
Implementation
Job scheduling
Resource sharing
First Come, First Serve (FCFS) systems
Stack vs Queue
| Stack | Queue |
| Stacks are based on the Last In First Out (LIFO) principle, i.e., the element inserted at the last, is the first element to come out of the list. | Queues are based on the First In First Out (FIFO) principle, i.e., the element inserted at the first, is the first element to come out of the list. |
| Insertion and deletion in stacks take place only from one end of the list called the top. | Insertion and deletion in queues take place from the opposite ends of the list. The insertion takes place at the rear of the list and the deletion takes place from the front of the list. |
| push() is used for the insertion | enqueue() is used for the insertion |
| pop() is used for deletion | dequeue() is used for deletion |
| In stacks, we maintain only one pointer to access the list, called the top, which always points to the last element present in the list. | In queues, we maintain two pointers to access the list. The front pointer always points to the first element inserted in the list and is still present, and the rear pointer always points to the last inserted element. |
Non-linear data structures
Non-linear data structures are arranged on multiple levels non-sequentially. The data structure focuses on efficient memory use but is harder to implement and traverse.
Tree

A tree is a non-linear data structure that implements a hierarchical relationship between elements. A tree consists of nodes and edges. Each node connects to many children, but every child has exactly one parent. An exception is the topmost node (root), which has no parents, and the bottom nodes (leaves), which have no children.
Binary tree
A typical family of tree-like data structures is a binary tree where every node has a maximum of two children (left and right). Binary trees help define many other practical data structures, such as binary search trees (BST), heaps, etc.
Resources to learn them:
Tree traversals
Inorder: Left subtree➡️root➡️right subtree
Preorder: root➡️left subtree➡️right subtree
Postorder: left subtree➡️right subtree➡️root

Implementation
- In structure representation, every node is represented by a structure and there are pointers which are pointing to the other nodes. It is the most popular representation. It works well for binary trees. But in the case of n-ary trees if the value of n is large then all the nodes might not have all the children. Hence having pointers at each node might be a waste of space. Here is a representation of a binary tree with a doubly linked list.

- In the first child/next sibling representation, at each node link for the children of the same parent(siblings) from left to right, remove the links from the parent to all children except the first child.
Since we have a link between children, we do not need extra links from parents to all the children. This representation allows us to traverse all the elements by starting with the first child of the parent. In the case of N-ary trees, it helps in saving a lot of memory.

- Array representation
It is most useful in case of heaps as if the tree is skewed then the size of the array required may increase up to (2^n - 1).

Applications of trees
Folder or directory structure
define other specialized data structures, such as disjoint sets, priority queues, etc.
In XML parser.
Machine learning algorithm.
For indexing in the database.
IN server like DNS (Domain Name Server)
In Computer Graphics.
To evaluate an expression.
In a chess game, it stores the defence moves of the player.
In java virtual machine.
As a workflow for compositing digital images for visual effects.
Decision trees.
Graph
With the advent of the internet, they represented the entire world wide web as a graph. Every webpage was represented as a node. A link between two web pages is represented as an edge.
Graphs are non-linear data structures consisting of vertices (nodes, points) connected by edges (links, lines).
In a tree, all the nodes are always connected. In a graph, all the nodes may not be always connected. If there is an edge between two nodes then they are called adjacent nodes.
Representation of graphs
- The adjacency matrix represents a graph through a two-dimensional (2D) array. The total number of vertices determines both dimensions. If the value in the matrix is 1, an edge exists between the two vertices.

An adjacency list uses an array of linked lists to represent a graph. An index represents every vertex, while the linked list contains all links to the vertex.

Which representation to use?
It depends on the type of graph.
If the graph is dense then matrix representation is preferred. This is because the matric will be properly utilized. This is because most of the cells will be 1s and hence space will be utilized properly.
If the graph is sparse then we go for adjacency list representation. In the case of sparse graphs if we use matrix representation then most of the values inside it will be 0s.
Applications of graphs
Google maps use graphs for building transportation systems
In Operating System, in the Resource Allocation Graph, each process and resource is considered to be vertices. Edges are drawn from resources to the allocated process, or from requesting process to the requested resource. If this leads to any formation of a cycle then a deadlock will occur.
In the mapping system, we use graphs. It is useful to find out which is an excellent place from the location as well as your nearby location. In GPS we also use graphs.
Facebook uses graphs to suggest mutual friends. It shows a list of the following pages, friends, and contact lists.
Microsoft Excel uses DAG (Directed Acyclic Graphs).
On social media sites, we use graphs to track the data of the users. liked showing preferred post suggestions, recommendations, etc.
Advanced Data Structures
Disjoint set
Resources
CS50x by David J. Malan, Harvard University - Course
Ravindrababu Ravula Sir's GATE lectures- YouTube
Geeks for geeks website
Introduction to Algorithms by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein - Book